Topographic VAEs learn Equivariant Capsules

in Research

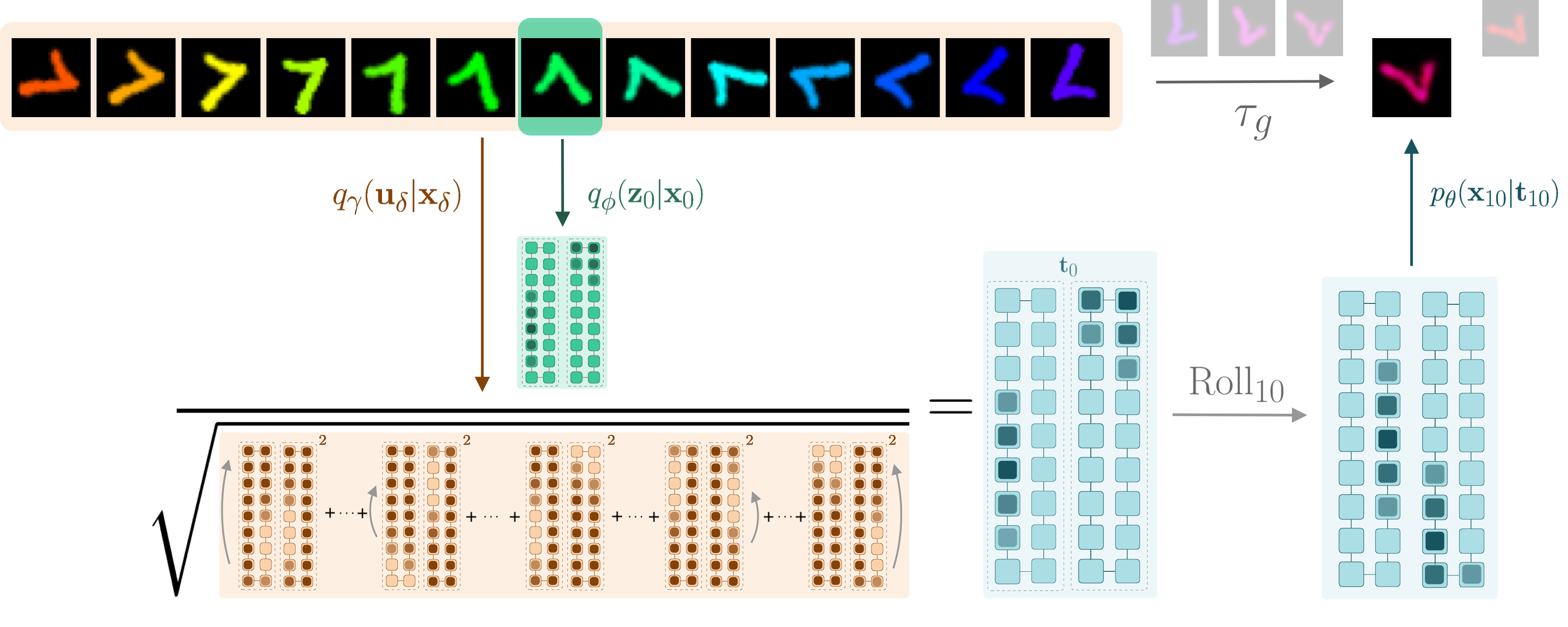Topographic VAE Overview Overview of the Topographic VAE with shifting temporal coherence. The combined color/rotation transformation in input space \(\tau_g\) becomes encoded as a \(\mathrm{Roll}\) within the equivariant capsule dimension. The model is thus able decode unseen sequence elements by encoding a partial sequence and rolling activations within the capsules. We see this completes a commutative diagram.

In this work we seek to bridge the concepts of topographic organization and equivariance in neural networks. To accomplish this, we introduce the Topographic VAE: a novel method for efficiently training deep generative models with topographically organized latent variables. We show that such a model indeed learns to organize its activations according to salient characteristics such as digit class, width, and style on MNIST. Furthermore, through topographic organization over time (i.e. temporal coherence), we demonstrate how predefined latent space transformation operators can be encouraged for observed transformed input sequences – a primitive form of unsupervised learned equivariance. We demonstrate that this model successfully learns sets of approximately equivariant features (i.e. “capsules”) directly from sequences and achieves higher likelihood on correspondingly transforming test sequences. Equivariance is verified quantitatively by measuring the approximate commutativity of the inference network and the sequence transformations. Finally, we demonstrate approximate equivariance to complex transformations, expanding upon the capabilities of existing group equivariant neural networks.

T. Anderson Keller, Max Welling

ArXiv Paper: https://arxiv.org/abs/2109.01394
Accepted at: NeurIPS 2021

Yannic Kilcher: https://www.youtube.com/watch?v=pBau7umFhjQ

Github.com/AKAndykeller/TopographicVAE

Video Summary

Tweet-print