DEUT -- 2D Structured and Approximately Equivariant Representations
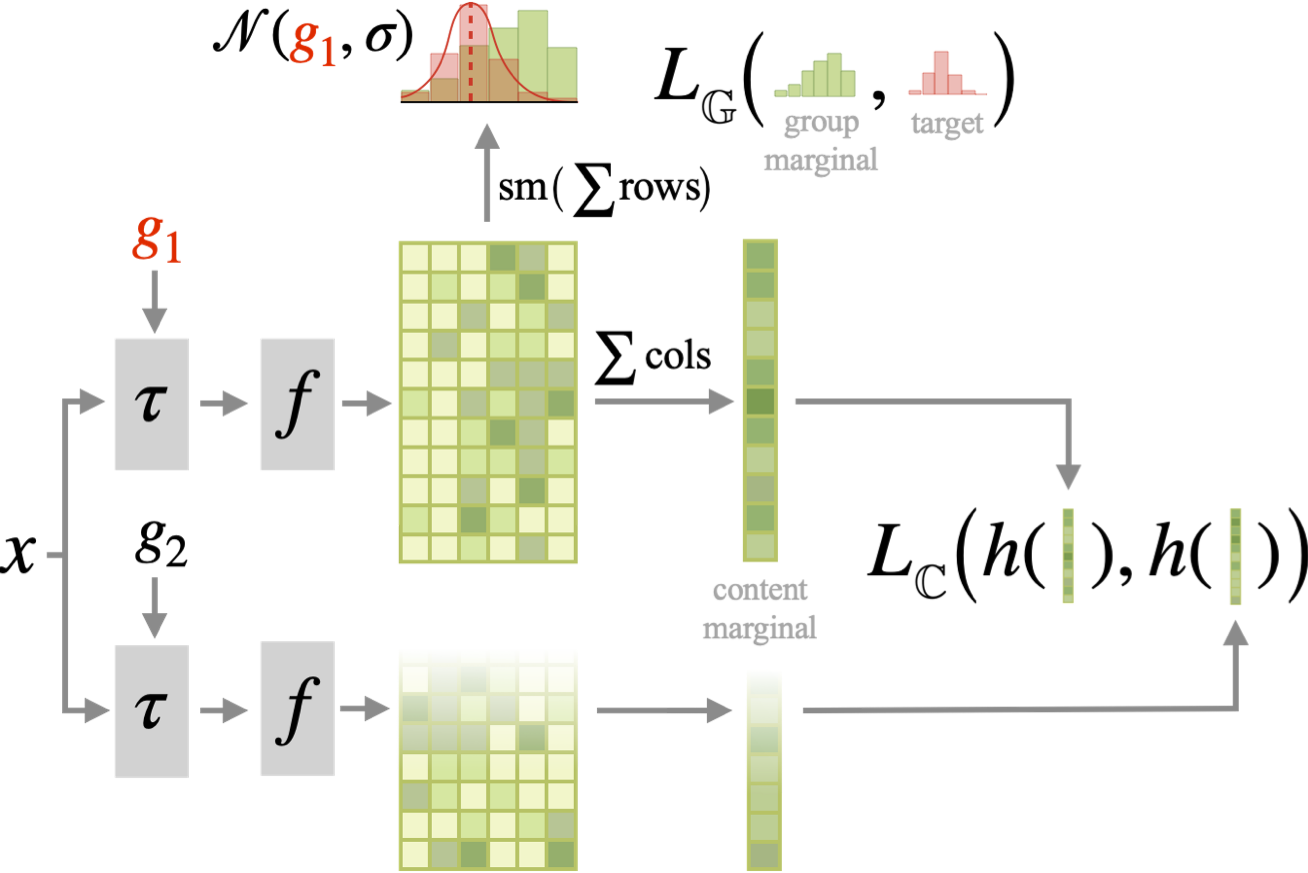Visualization of the DUET framework. The backbone \(f\) yields a 2d representation for each transformed image \(f(\tau_g(\mathbf{x}))\) (e.g. \(\tau_g\) is a rotation by \(g\) degrees). The group marginal is obtained as the softmax (sm) of the sum of the rows, and is compared to the prescribed target (red) with our group loss \(L_G\). The content is obtained by summing the columns, and contrasted (\(L_C\)) with the other view through a projection head \(h\). The final representation for downstream tasks is the 2d one, which has been optimized through its marginals.
Multiview Self-Supervised Learning (MSSL) is based on learning invariances with respect to a set of input transformations. However, invariance partially or totally removes transformation-related information from the representations, which might harm performance for specific downstream tasks that require such information. We propose 2D strUctured and EquivarianT representations (coined DUET), which are 2d representations organized in a matrix structure, and equivariant with respect to transformations acting on the input data. DUET representations maintain information about an input transformation, while remaining semantically expressive. Compared to SimCLR (Chen et al., 2020) (unstructured and invariant) and ESSL (Dangovski et al., 2022) (unstructured and equivariant), the structured and equivariant nature of DUET representations enables controlled generation with lower reconstruction error, while controllability is not possible with SimCLR or ESSL. DUET also achieves higher accuracy for several discriminative tasks, and improves transfer learning.
Xavier Suau, Federico Danieli, T. Anderson Keller, Arno Blaas, Chen Huang, Jason Ramapuram, Dan Busbridge, Luca Zappella
Accepted at ICML 2023: https://arxiv.org/abs/2306.16058