Unsupervised Representation Learning from Sparse Transformation Analysis
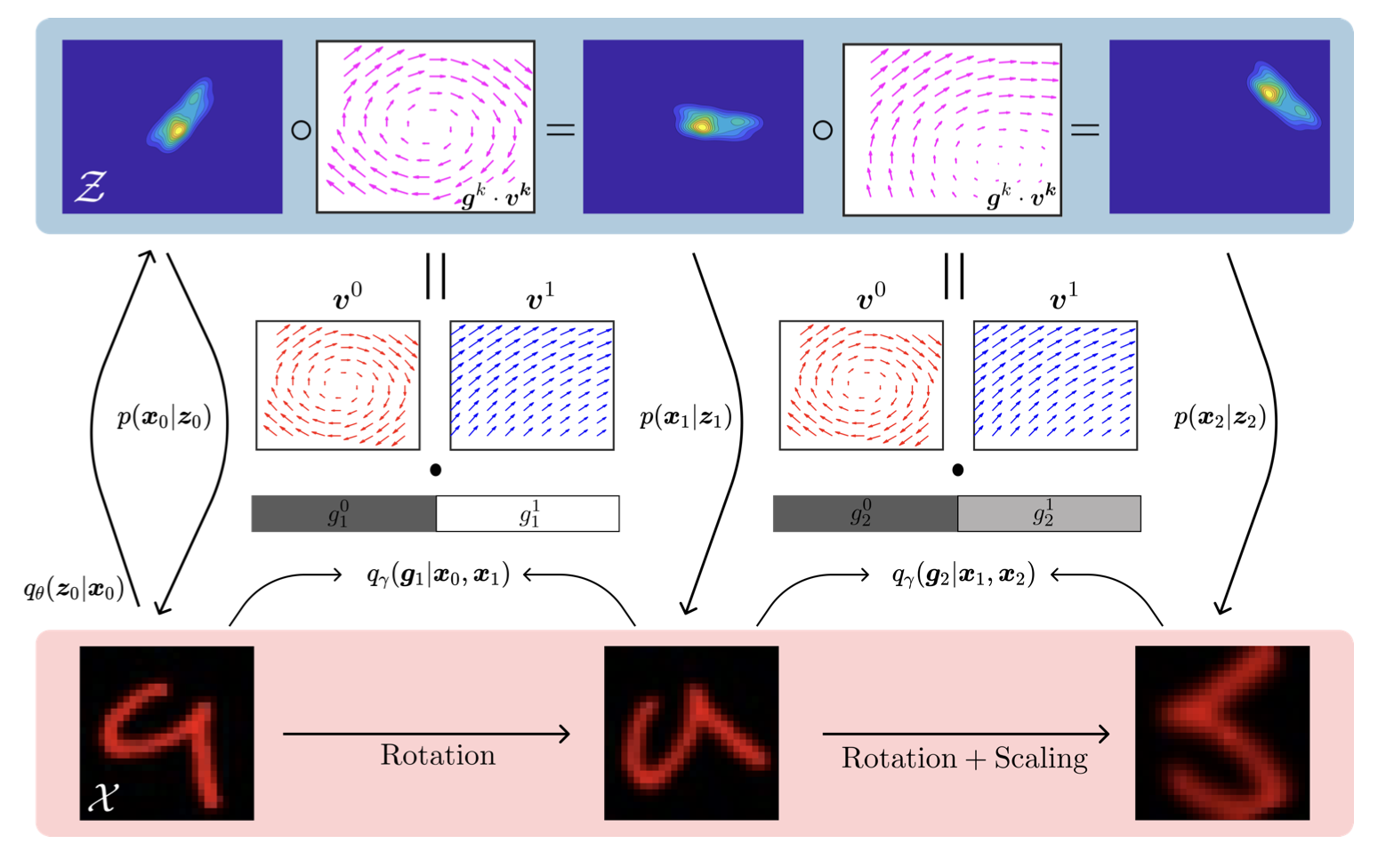 We learn representations from sequence data by factorizing latent transformations into sparse flow components, yielding disentangled transformation primitives and approximately equivariant structure.
We learn representations from sequence data by factorizing latent transformations into sparse flow components, yielding disentangled transformation primitives and approximately equivariant structure.
There is a vast literature on unsupervised representation learning based on principles such as coding efficiency, statistical independence, causality, controllability, and symmetry. In this work, we propose to learn representations from sequence data by explicitly modeling how latent variables transform over time, and by factorizing those transformations into a sparse set of components. Inputs are encoded as distributions over latent activations, then evolved forward using a probability flow model before decoding to predict a future input state. The flow model is decomposed into rotational (divergence-free) and potential (curl-free) vector fields, and a sparsity prior encourages only a small number of these fields to be active at any instant while inferring the speed of probability flow along them. Training is completely unsupervised via a standard variational objective, and results in a new form of disentanglement: inputs are represented not only by independent latent factors, but also by independent transformation primitives given by learned flow fields. Interpreting these transformations as symmetries, the resulting representations can be viewed as approximately equivariant. Empirically, the model achieves strong performance in both data likelihood and unsupervised approximate equivariance error on datasets composed of sequence transformations.
Yue Song, T. Anderson Keller, Yisong Yue, Pietro Perona, Max Welling
Accepted at IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI)
Paper: https://arxiv.org/abs/2410.05564