A Spatiotemporal Perspective on Dynamical Computation in Neural Information Processing Systems
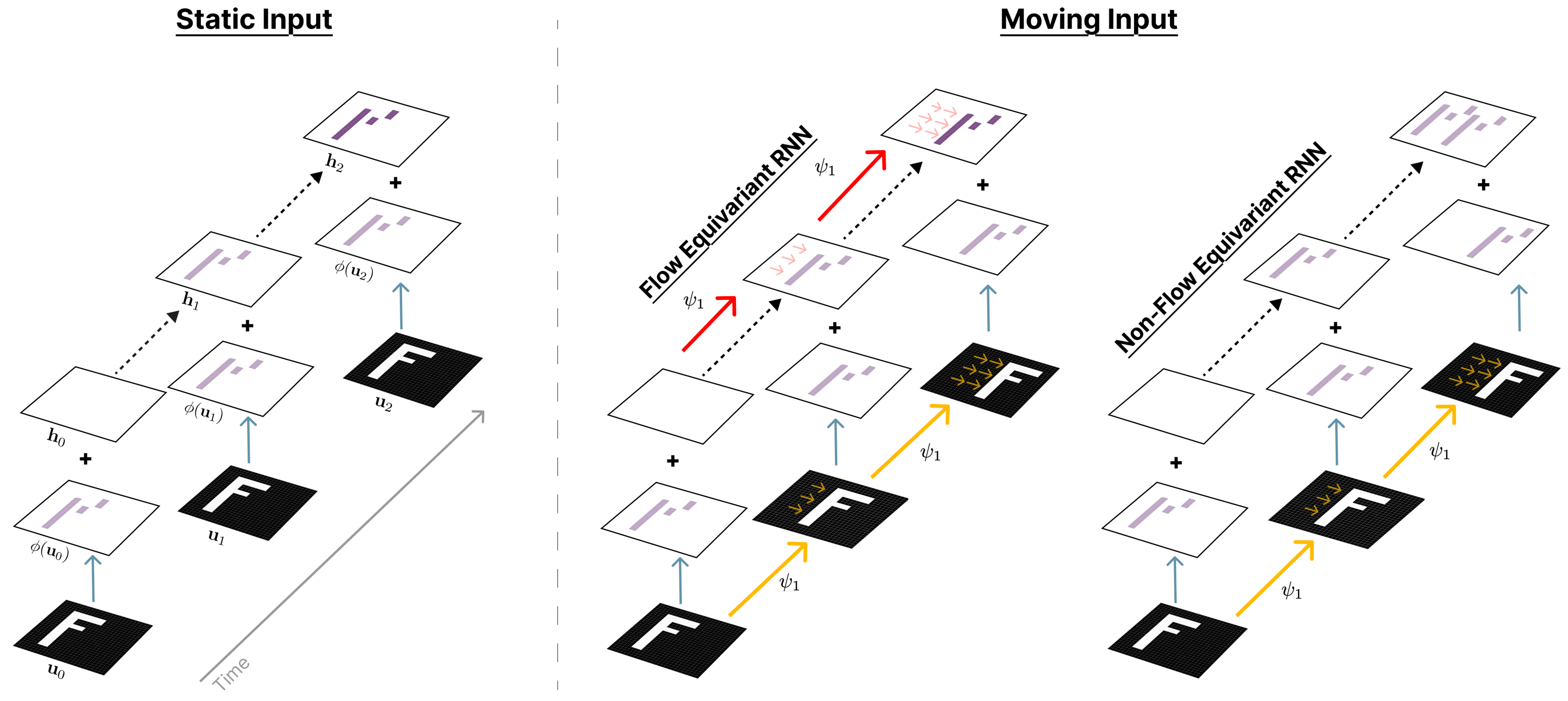A flow equivariant neural network will process a moving stimulus sequence the same way as it processes a static stimulus sequence, but with the same motion applied to its hidden state. To achieve this property for a specific input flow $\psi^{(\nu)}$, a corresponding flow must preemptively shift the hidden state before the input comes in (denoted by red arrows).
Spatiotemporal flows of neural activity, such as traveling waves, have been observed throughout the brain since the earliest recordings; yet there is still little consensus on their functional role. Recent experiments and models have linked traveling waves to visual and physical motion, but these observations have been difficult to reconcile with standard accounts of topographically organized selectivity and feedforward receptive fields. Here, we introduce a theoretical framework that formalizes and generalizes the connection between ‘motion’ and flowing neural dynamics in the language of equivariant neural network theory. We consider ‘motion’ not only in physical or visual spaces, but also in more abstract representational spaces, and we argue that recurrent traveling-wave-like dynamics are not just useful but necessary for accurate and stable processing of any signal undergoing such motion. Formally, we show that for any non-trivial recurrent neural network to process a sequence undergoing a flow transformation (such as visual motion) in a structured equivariant manner, its hidden state dynamics must actively realize a homomorphic representation of the same flow through recurrent connectivity. In this “spatiotemporal perspective on dynamical computation”, traveling waves and related flows are best understood as faithful dynamic representations of stimulus flows; and consequently the natural inclination of biological systems towards such dynamics may be viewed as an innate inductive bias towards efficiency and generalization in the spatiotemporally-structured dynamical world they inhabit.
T. Anderson Keller, Lyle Muller, Terrence Sejnowski, and Max Welling
Preprint (under review): https://arxiv.org/abs/2409.13669