Block Recurrent Dynamics in Vision Transformers
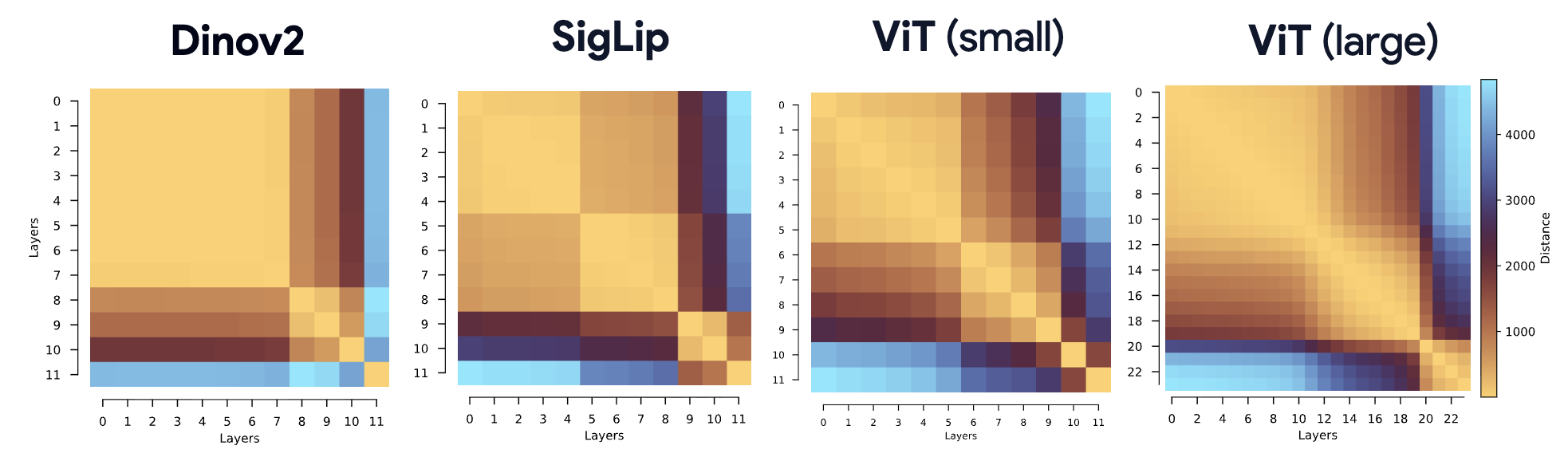 Layer–layer similarity matrices across diverse Vision Transformers reveal block structure. We propose the Block-Recurrent Hypothesis: trained ViTs can be rewritten using only k ≪ L distinct blocks applied recurrently, enabling a program of dynamical interpretability.
Layer–layer similarity matrices across diverse Vision Transformers reveal block structure. We propose the Block-Recurrent Hypothesis: trained ViTs can be rewritten using only k ≪ L distinct blocks applied recurrently, enabling a program of dynamical interpretability.
As Vision Transformers (ViTs) become standard backbones across vision, a mechanistic account of their computational phenomenology is now essential. Despite architectural cues that hint at dynamical structure, there is no settled framework that interprets Transformer depth as a well-characterized flow. In this work, we introduce the Block-Recurrent Hypothesis (BRH), arguing that trained ViTs admit a block-recurrent depth structure such that the computation of the original L blocks can be accurately rewritten using only k ≪ L distinct blocks applied recurrently. Across diverse ViTs, between-layer representational similarity matrices suggest few contiguous phases. To determine whether this reflects reusable computation, we operationalize our hypothesis in the form of block recurrent surrogates of pretrained ViTs, which we call Recurrent Approximations to Phase-structured TransfORmers (Raptor). Using small-scale ViTs, we demonstrate that phase-structure metrics correlate with our ability to accurately fit Raptor and identify the role of stochastic depth in promoting the recurrent block structure. We then provide an empirical existence proof for BRH in foundation models by showing that we can train aRaptor model to recover 94% of DINOv2 ImageNet-1k linear probe accuracy in only 2 blocks. To provide a mechanistic account of these observations, we leverage our hypothesis to develop a program of Dynamical Interpretability. We find (i) directional convergence into class-dependent angular basins with self-correcting trajectories under small perturbations (ii) token-specific dynamics, where clsexecutes sharp late reorientations while patch tokens exhibit strong late-stage coherence reminiscent of a mean-field effect and converge rapidly toward their mean direction and (iii) a collapse of the update field to low rank in late depth, consistent with convergence to low-dimensional attractors. Altogether, we find that a compact recurrent program emerges along the depth of ViTs, pointing to a low-complexity normative solution that enables these models to be studied through principled dynamical systems analysis.
Mozes Jacobs, Thomas Fel, R. Hakim, A. Brondetta, Demba E. Ba, T. Anderson Keller
ArXiv: https://arxiv.org/pdf/2512.19941
OpenReview: https://openreview.net/forum?id=gH3HhnfWLC
Accepted at ICLR ‘26